Introduction

NARS takes a single major technique to carry out various cognitive functions and to solve various problems. This technique enables to model any aspect of an intelligent system – perception, cognition, reasoning, consciousness … in a unified way.

Dr. Pei Wang already published many papers about the NARS capabilities, most notably, the one about problem solving case-by-case manner without using a known algorithm.

In this article I would like to demonstrate that NARS can be used as well for other task without using a special module, technique or tool attached to a system.

NARS is ideal for dealing with perception for many reason. As it with the problem solving, when there is an absence of an exact algorithm to solve the (even a very simple) problem, in perception, problems occur with information ambiguity (inverse optics problem), its correctness (source of information might infer with other sources) and completeness.
So some information might be lost, some are not accurate, and even though having everything right, the interpretation and importance of any perceived information is system dependent.

The following diagram shows the common framework for state-of-the-art ASR (Automatic Speech Recognition) systems, which has been fairly stable for about two decades now and a proposed ASR using NARS.

A transformation of a short-term power spectral estimate is computed every 10ms, and then is used as an observation vector for Gaussian-mixture-based HMMs that have been trained on as much data as possible, augmented by prior probabilities for word sequences generated by smoothed counts from many examples.

Many feature extraction methods, that have been used for automatic speech recognition (ASR) have either been inspired by analogy to biological mechanisms, or at least have similar functional properties to biological or psycho-acoustic properties for humans or other mammals.

The most common features used today in ASR systems are MFCC (Mel-scale Frequency Cepstral Coefficient). For non-speech audio classification purposes, or to improve accuracy, also other audio features are commonly used or their combination. The following chapter shows simple steps how to obtain MFCC from audio signal.

---

Calculating (MFCC) audio features

Input analog signal x(t) is converted to a discrete valued discrete time signal s[n] at a sample rate f.

Bellow, some simple steps shows, how to obtain MFCC (Mel Frequency Cepstral Coefficients) from this converted audio signal^1,2.

Step 1: Pre–emphasis

To compensate the high-frequency part that was suppressed during the sound production mechanism of humans and also to improve signal-to-noise ratio, audio signal are passed through the high pass filter.

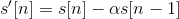
Step 2: Framing

The signal is then framed into small chunks with some overlap. Usually the frame width is 25ms with an overlap 10ms.

Step 3: Hamming windowing

In order to apply spectral analysis to a frame, it has to be multiplied with a window, to keep the continuity of the first and the last point and avoiding “spectral leakage”.

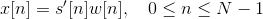
Hamming window is defined as:

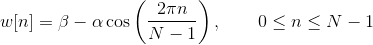
, where N represents the width, in samples, of a discrete-time.

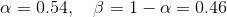
Step 4: Fourier transform of the signal

FFT is performed to obtain the magnitude frequency response of each frame. Spectral analysis shows that different timbres in speech signals corresponds to different energy distribution over frequencies.

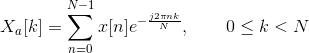
Step 5: Mel Filter Bank Processing

Non-linear frequency scale is used, which approximates the behaviour of the auditory system. The mel scale is a perceptual scale of pitches judged by listeners to be equal in distance from one another.

The mel-scale B and its inverse B^-1 can be given by Eq (different authors use different formulas):

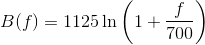
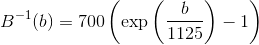
We define a filter bank with M filters, where filter m is triangular filter given by:

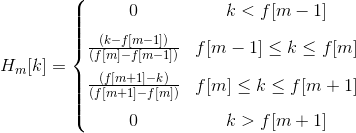
Such filters compute the average spectrum around each center frequency with increasing bandwidths.

Let’s define f_l and f_h to be the lowest and highest frequencies of the filter bank in Hz, F_s the sampling frequency in Hz, M the number of filters, and N the size of the FFT. The boundary points f[m] are uniformly spaced in the mel-scale:

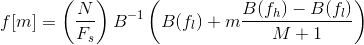
Step 6: Discrete Cosine Transform

We then compute the log-energy at the output of each filter as

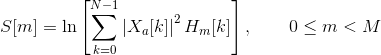
The mel frequency cepstrum is then the discrete cosine transform of the M filter outputs:

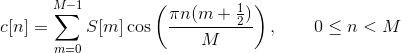
Discrete cosine transform decorrelates the features (improves statistical properties by removing correlations between the features).

Step 6: Feature vector

The energy within a frame is also an important feature that can be easily obtained. Hence we usually add the log energy as the 13rd feature to MFCC. If necessary, we can add some other features at this step, including pitch, zero cross rate, high-order spectrum momentum, and so on.

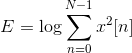
It is also advantageous to have the time derivatives of (energy+MFCC) as new features as velocity and acceleration coefficients (which are simply the 1st and 2nd time derivative of cepstral coefficients respectively).

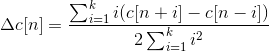
Together with delta (velocity) and delta-delta (acceleration) coefficients, represents the audio feature vector used in conventional ASR..

---

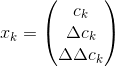
Representing audio features in Narsese

All the stages so far, shared common parts in conventional and ASR using NARS. Conventional ASR uses HMM (Hidden Markov Model) in next stages which incorporates acoustic and language models.

While numerical representation of feature facilitate processing and statistical analysis in conventional ASR (real numbers, fixed information structure), which is appropriate given its statistical nature, in NARS however, features needed to be converted to Narsese. Two questions arise here:

• How to represent numerical values?
• How to represent temporariness of attributes?

It would be possible to use other modules attached to NARS and do numerical calculations, but this is what tried to be avoided from the beginning.

Representing numerical values

Usually, there is no need to represent exact numerical values in perception unless we want to represent numbers itself. In perception the accuracy of recognition is not necesarilly proportional to accuracy of received information. If we were a green-tinted glasses or replace our white light bulb with a green one, we will notice the tint, but we still identify bananas as yellow, paper as white, walls as brown (or whatever), and so forth. So the wavelengths of light does not correspond to colours we experience (or we want the system to experience) no matter how accurately we perceive it. The same information might be seen differently dependent on certain conditions and the system previous experience.

To be able to uniquely identify and classify certain information or object, we need to choose the right features. While some of them should be similaritive (invariant to certain properties) to classify as the same category of objects, others, should be distinctive, to uniquely identify object within the same class. There is no need an exhaustive list of all features we can gather nor concentrating to get it as precisely as we can (anyway we would not get it right - as it implies from the mentioned example above). So not the number of coefficients and its accuracy, but rather the character of features, its adaptive choice based on current conditions and the amount of experience and its variety the system has what matters the most.

Representing temporal attributes

The validity of information (statements - in NARS terminology) might be time dependent. In Pei Wang's NARS design, there are tree mechanism to deal with temporal statements³.

• Relative representation. Some compound terms (implication, equivalence, and conjunction) may have temporal order specified among its components.
• Numerical representation. A sentence has a time stamp to indicate its "creation time", plus an optional "tense" or its truth-value, with respect to this time.
• Explicit representation. When the above representations cannot satisfy the accuracy requirement when temporal information is needed, it is always possible to introduce terms to explicitly represent an event or a temporal relation.

The explicit representation is the most basic one, since it doesn’t requires to implement temporal inference rules, but time and events are expressed as terms. The first approach is not implemented yet in the library presented on this site, but a limited version of second - numerical representation of temporal statements is implemented with following properties:

• The temporal statement is indicated by a tense (currently just "|⇒", which represents a present tense by Wang's NAL) and a time stamp is attached to it to represent the creation time.
• Every temporal statement keeps its truth value for a short period of time after which the statement is discarded from the system.
• It is still a way to remember a whole history of temporal statements, by (periodically) assigning the value to a new term before it gets discarded.
• Any statement derived from a temporal statement is also temporal.

The advantage of temporal statements to represent features in perception this way is, that system does not have to update the states of all those features, whenever their change. Remember, that in conventional ASR, the whole feature vector are feeded into system by every frame, which also limits the amount of features used in the system. However in NARS by the next frame, temporal features from previous frame are already deprecated, so the actual list of used features might differ from frame to from, and it is not limited either by number or type.

---

Possible implementation

This chapter shows a working demonstration, how such a system could be implemented. For simplicity, it will be explained just on recognising vowels, given, this is one of the simplest task in speech recognition process.

This demonstration uses NARS library available on this website together with FFTW library which handles calculation of audio features from the input signal. The test program was able to process in real-time requiring very little computer resources.

The following charts are based on this audio recording of words with General American English vowels illustrated on Table 1.

Table 1 General American English vowels

	b__d	IPA		b__d	IPA
1	bead	iː	9	bode	oʊ
2	bid	ɪ	10	booed	uː
3	bayed	eɪ	11	bud	ʌ
4	bed	ɛ	12	bird	ɜː
5	bad	æ	13	bide	aɪ
6	bod(y)	ɑː	14	bowed	aʊ
7	bawd	ɔː	15	Boyd	ɔɪ
8	budd(hist)	ʊ

A certain threshold of log energy of a frame can be used to indicate of the beginning and the end of a word thus the processing.

Figure 2 Log Energy of each frame (x-frame number, y-log energy of a frame)

On Figure 3, one could notice, that the energy level of bands (for clarity is shown just the first four), represented by cepstral coefficients within a vowel are quite constant. One possible solution to recognise them could be to either measure the value of each cepstral coefficient (which is tried to be avoid, as it was mention in the chapter about the numerical representation) or measuring their relative order to each other. But that could be also misleading, since not the actual values but rather the positions of frequency bands with high (and low) energy what matters. Depending on the speaker, this might also slightly change, so having more Narsese rules for every vowel could be very handy. Moreover, we might get also information about the speaker (high or low pitch voice, gender etc.).

Figure 3 Vowels and their mel scale cepstral coefficients

Figure 4 is the same recording showing the values of coefficients, but from different perspective. Here, the time is static (in vowels the cepstral coefficient are not time dependant), and showing the value of cepstral coefficients for different vowels (we would like to differentiate one vowel from others). This chart clearly show, that just by featuring maxima and minima, we could uniquely identify vowels.
As for consonants, we would need to take to account the time dependant coefficients (velocity and acceleration).

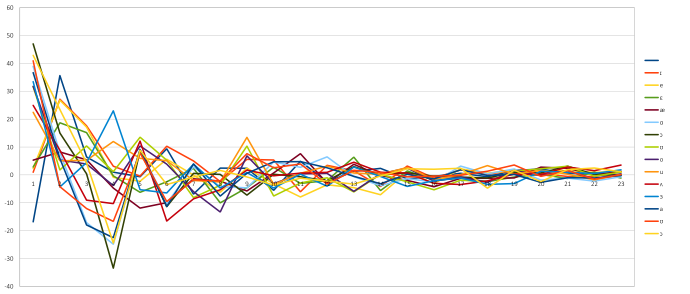
Figure 4 Vowels and their mel scale cepstral coefficients (x-cepstral coefficient, y-log energy)

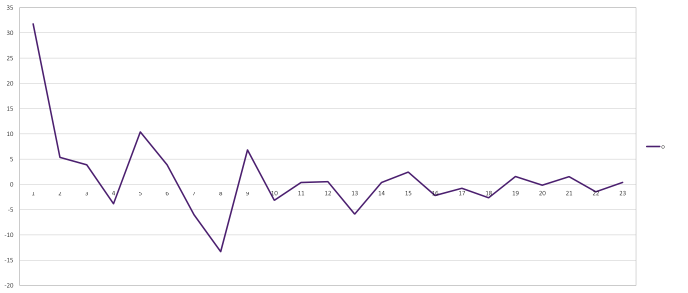
Figure 5 Vowel "o" and its mel scale cepstral coefficients (taken from Figure 4)

Code 1 Vowel "o" and its features in Narsese

Code 1 shows a possible representation of vowel 'o' in Narsese. Every vowel could have multiple rules attached to it and also rules to recognise other attributes of speech, like pitch, intonations etc..

Code 2 Representing all the vowels from Table 1 in Narsese

Code 3 Vowel "o" represented in Narsese

Code 4 Same as in Code 3, but with default truth values

Code 5 an example question asked after features are entered to the system by every frame.

Code 2 representing a knowledge base needed for speech processing, and which is already stored in the system, and Code 3 or Code 4 and Code 5 is an example, how features might be converted to Narsese and sent to the system by every frame.

So the basic concept is, that system would contain knowledge about the language (similarly to acoustic and language model in conventional ASR) in Narsese and features would enter to the system (also in Narsese) together with some questions and/or goals. Than system would provide some answers and perhaps actions. A full featured ASR would require much more sophisticated rules than it was shown previously and also there arise a question, how to automatically build such a knowledge base.

But the advantage could be huge. The knowledge is shared in the whole system, so also information coming from other type of sensory sources could be used. The same system could be used also for visual perception or for controlling sensory motors. Also, system could use active sensors to better adapt to current conditions and surrounding environment.

1. Xuedong Huang, Alex Acero, Hsiao-Wuen Hon (May 5, 2001), Spoken Language Processing: A Guide to Theory, Algorithm and System Development
2. Roger Jang (張智星), Audio Signal Processing and Recognition
3. Pei Wang (May 6, 2013), Non-Axiomatic Logic: A Model of Intelligent Reasoning

• Prev